2D 碰撞檢測包圍盒

發表於 2025-05-24 分類於 2D Physics

在碰撞檢測中可以分為兩個階段 Broad-Phase 和 Narrow-Phase，在 Broad-Phase 中先進行粗略的篩選可能碰撞的物體，之後才會在 Narrow-Phase 做精細的計算判斷兩物體是否產生碰撞。

為何需要分為兩個階段進行？假設場景中有兩顆球在移動，如果要判斷兩球是否產生碰撞，一顆球只需計算和另一顆球的碰撞，若有三顆球則變為兩次，以此類推若有 N 顆球則每顆球需要計算 N-1 次，計算複雜度為 $\mathcal{O(N^2)}$ ，這樣的計算量顯然是不能使用的，因此需要 Broad-Phase 先對物體進行篩選。

在 Broad-Phase 通常會先將物體簡化為包圍盒，常見的包圍盒有 AABB(Axis-Aligned Bounding Box)、OBB(Oriented Bounding Box) 等，同時使用四叉樹(QuadTree)、BVH(Bounding volume hierarchy) 等技術將物體所在的空間作分割達到減少計算量的目的。

本文將介紹 AABB、OBB 這兩種包圍盒。

1. AABB(Axis-Aligned Bounding Box)

AABB 顧名思義就是按照和座標軸對齊的包圍盒，四個邊都會和座標軸對齊，因此只需要圖形在座標軸上的極大值與極小值就可以生成一個 AABB，如下圖。

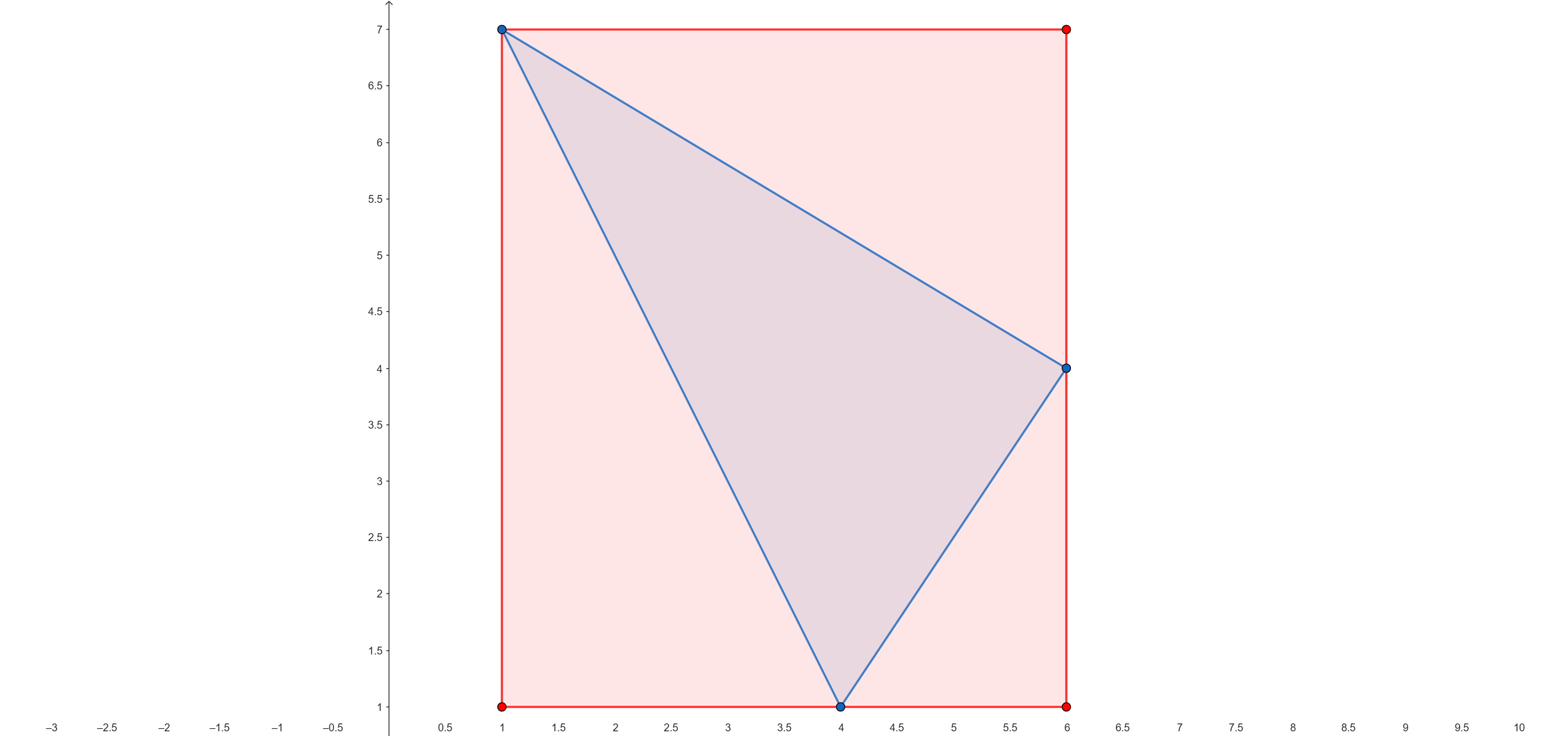
藍色三角形的 AABB 就是紅色矩形。

AABB 的碰撞檢測也很簡單，兩個圖形在每一個座標軸上的投影都會產生重疊，如下圖。

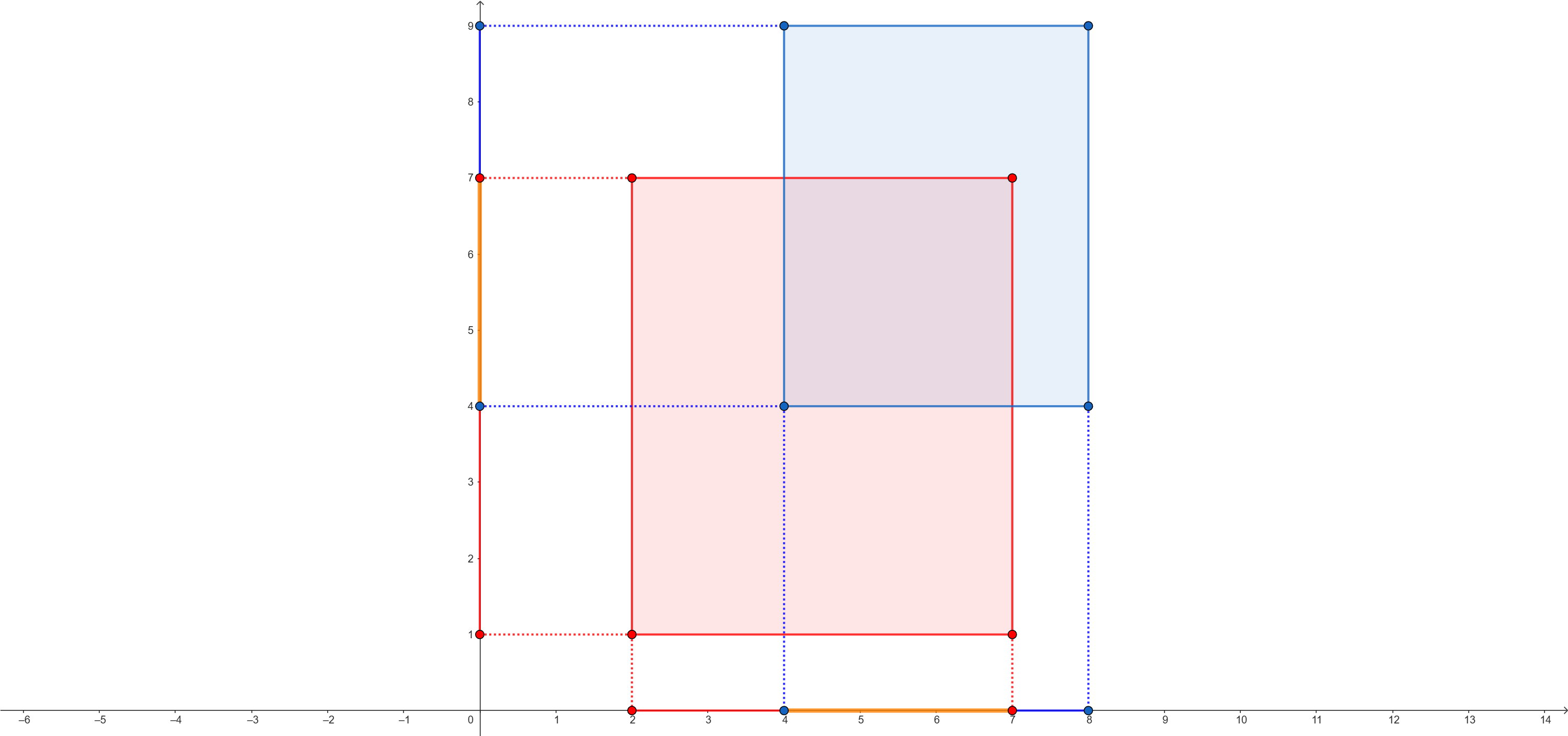
橘色線段即兩包圍盒在座標軸上重疊的部分。

假設有一包圍盒 $A$ 的頂點分別是 $(x_1, y_1) ,\space (x_2, y_2)$ 且 $x_1 < x_2 ,\space y_1 < y_2$ ，和另一包圍盒 $B$ 發生碰撞，包圍盒 $B$ 則會有一頂點 $(x, y)$ 在包圍盒 $A$ 的內部，滿足以下條件 $x_1 \eqslantless x \eqslantless x_2 ,\space y_1 \eqslantless y \eqslantless y_2$ 。

AABB 在碰撞檢測的計算上十分快速，但有一個缺點，因為四個邊都是和座標軸對齊的，一旦圖形產生旋轉，頂點無法直接同時旋轉使用，必須重新計算新的頂點。

2. OBB(Oriented Bounding Box)

OBB 定向包圍盒，和 AABB 相似，包圍盒的形狀都是一個矩形，但是具有方向性，可以旋轉，生成的方式較 AABB 複雜，會先透過如 PCA(Principle Component Analysis) 等演算法找到適合的軸線，再計算圖形在座標軸上的極大值與極小值，如下圖。

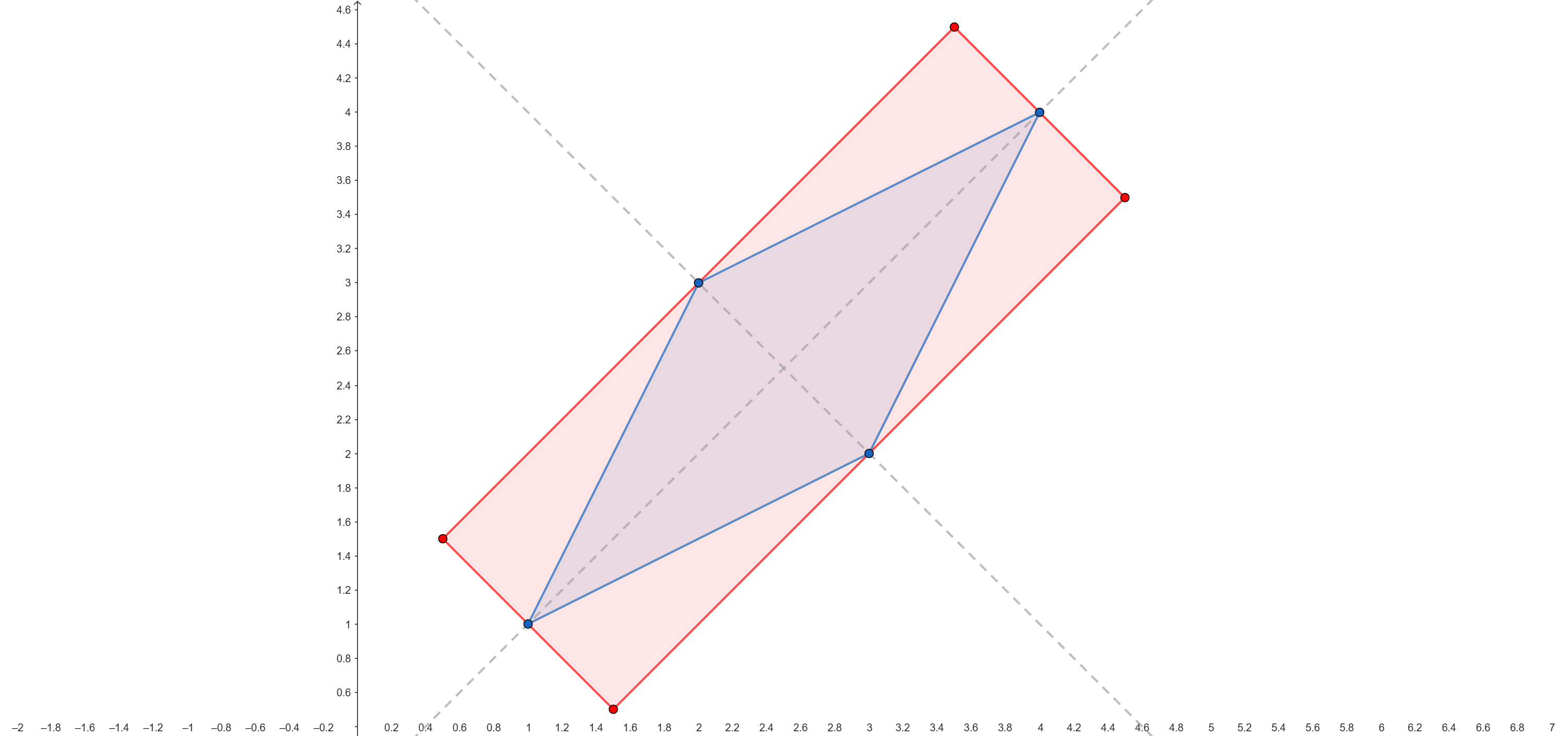
若以兩灰色軸線為 XY 軸，那就是一個 AABB。

OBB 的碰撞檢測更加複雜，由於圖形經過了旋轉，AABB 的檢測方法並不能滿足需求，就需要用到 SAT(Separating Axis Theorem)、GJK(Gilbert–Johnson–Keerthi) 等演算法，計算上的開銷比起 AABB 較大，因此 OBB 較適合使用在 Narrow-Phase 而不是 Broad-Phase。

參考資料